图论

当你读到标题中的图形这个词时，你首先想到的是什么?我打赌它是一个类似于这样的饼状图:

…或者是一个函数的图像:

…或者像这样的直方图:

但是，也许令人惊讶的是，在本文中，我们不会讨论这些“图”中的任何一个，而是讨论一种截然不同的图。首先让我来描述一下这些神奇的物体。在数学中，图是一个非常简单的结构，仅由顶点和边组成，这些顶点相互连接。图论是探索这些结构性质的数学领域。更诗意的名称经常用于图的基本组成部分，如“节点”或“点”的顶点，和“弧”或“线”的边。

既然图表如此简单，你可能会想，有没有一种简单的方法可以直观地表示它们，这样我们就不必在思考抽象对象时失去理智了?答案是:“当然”。这就是为什么它这么酷!我们可以很容易地画出任何图形。

现在，当我们知道如何绘制图形时，我们可能会想到它们可以在实际中使用的方法。很明显，它们可以完美地描述任何种类的物体之间的关系。例如，如果我们想象顶点代表人，那么边可以告诉我们这些人之间的友谊是什么(想想Facebook、Instagram或Twitter这样的社交网络)。另一个使用图形的模型是道路网络的表示，用顶点表示城市，用边缘表示道路。此外，图形还用于概率论、计算机科学、神经网络建模、人工智能、经济学、化学和许多其他科学:

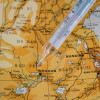
回到一个理论或发明的源头，回到一切开始的地方，总是令人兴奋的。让我们来到1735年的俄罗斯城市柯尼斯堡。我们和著名的瑞士数学家莱昂哈德·欧拉在一起，我们决定一起去散步。这是一张城市地图:

正如你所看到的，这个城市有七座桥。欧拉现在问你一个非常棘手的问题:“我的朋友，我们能不能在每座桥都过一次的情况下回到起点?”仔细想想，在城市里漫步一番，你会不得不承认，你找不到这样的散步方式。他肯定会告诉你为什么这是不可能的，因为他解决了这个问题，后来成为图论的开端。欧拉自己并没有使用图这个词，但它是后来由詹姆斯·约瑟夫·西尔维斯特引入的。

图论的另一个令人惊讶的应用是地图着色问题。19世纪的地理学家和历史学家很难掌握世界各国之间的边界现状。他们用来明确划分两个邻国的一种方法是，现在仍然是用不同的颜色来代表它们。但很快一个有趣的问题出现了:用这种方法给地图上色的最少颜色是多少?事实证明，这个问题比你想象的要困难得多，数学家花了100多年的时间才解决。1970年由Kenneth Appel和Wolfgang Haken提出的著名的四色定理被认为是数学逻辑推理的一个重要转折点，因为它是第一个用计算机证明的定理。

另一个关于图形着色问题的著名例子是流行的游戏“数独”。这两个问题都可以很容易地转化为图论问题，统称为顶点着色问题。

如今，图论的主要应用是在计算机科学和编程中，特别是在解决优化问题的算法设计中。在这类问题中，顾名思义，我们需要构建最优的——即最便宜或最有利可图的——做事方式。例如，假设我们要去某个遥远的度假胜地度假。为了到达那里，我们必须穿过许多城市，这些城市与许多道路相连，每条道路都有使用成本。我们想把旅行的费用降到最低，这样我们就能把最多的钱花在度假上。这个问题是用“加权”图来建模的，我们给每条边赋一个正值，代表那条路的成本(权重)。它被称为最短路径问题，因为我们的目标是最小化路径的总距离(用我们的术语来说就是成本)，并且很多算法都能非常有效地解决这个问题，包括Dijkstra和Bellman-Ford算法。

在这个简短的图论概述的最后，我们将考虑这个领域中最有趣和最具挑战性的问题。下面两个问题很容易描述，但要完全解决却要复杂得多。第一个描述了每个旅行推销员经常面临的问题，即如何在返回仓库之前选择他需要访问的地点之间的最短路线。找到近似解相对容易，但没有一种算法可以在合理的时间内为每个图给出确切的答案。这个令人惊讶的事实的原因是，随着我们在图中添加的每个新位置，可能的路线数量会以极快的速度增长(甚至超过指数!)。

旅行商问题(TSP)是NP-hard问题的一个例子，即“非确定性多项式”算法复杂度类。另一方面，邮递员也有非常相似的问题。为了把邮件送到每家每户，他们应该走遍城市的每一条街道。他们的目标是将路线的距离或成本最小化。这个问题被称为中国邮差问题，并且已经找到了在多项式时间内解决这个问题的算法，因此这个问题被认为是足够有效地解决的。

综上所述，我们必须指出图形在人工智能研究中的广泛应用，这被认为是不久的将来最伟大的科学和技术研究领域。甚至Siri和Cortana自己也使用一种称为决策树的图表来做出明智的选择……